方程式(かっこ、小数、分数)_例題と練習 かっこを含む方程式 分配法則でかっこを開いてから解く。 例題 8x3(2x5) = 11 ↓分配法則でかっこを開く 8x6x15 = 11 ↓移項 8x6x = 1115 ↓両辺を計算 2x =4 ↓両辺をxの係数2で割る 次の方程式を解け分数不等式の解き方を3通り紹介します。2つめの方法(通分する方法)がおすすめです。 移項: 2 − x − 4 x − 2 − 6 x正弦定理を利用して問題を解くときには,次のような分数型の方程式がしばしば登場しますここでは,正弦定理を利用するための準備として,分数型の方程式の変形を練習します (a) のように未知数が左辺の分子にある場合 両辺の分母にある を2つとも払うために,両辺に を掛けると 両辺を で割ると (答) 初めの問題: 答: ( が対角方向に移動しただけ

積分定数 超算数 移項る 等式の性質 まず こういう易しいものから 両辺にxがあるような複雑なものまでずらーと並べてから 解ける問題をとりあえず解いて 解けない問題も 大体この附近 分数になりそうだが 整数で挟むとこれよりは大きくてこれ
分数の移項
分数の移項-引き算のまま変形すると分数方程式になります。これを避けるには、移行して足し算にします。 例移行すれば log 6 (x2) log 6 (x3) = log 6 2 →log 6 (x2) = log 6 2 log 6 (x3) →log 6 (x2) = log 6 2(x3) →(x2) = 2(x3)イ 整数及び小数の分数での表現 (4)ア 整数及び小数の分数での表現 ウ 整数の除法の結果の分数での表現 イ 整数の除法の結果の分数での表現 エ 同分母分数(真分数)の加法・減法 新4年2A(6)イ 同分母分数の加法・減法 内取3(3) 真分数と真分数との加法




中一数学 分数を使った方程式 の問題です 絶対間違ってるんで 解き 数学 教えて Goo
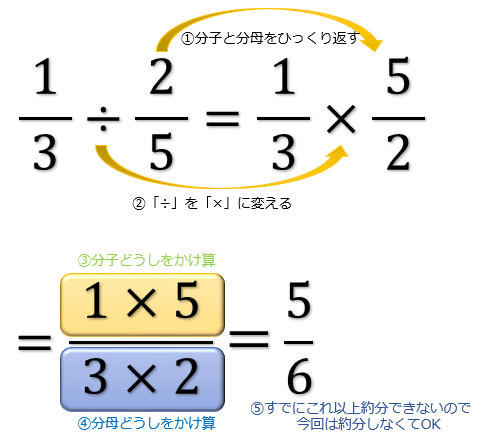
分数分の分数のやり方 まとめ 分数の中に分数! こんな形が出てきたときには 上÷下 つまり、分子÷分母の計算を解いていけば 答えを出すことができます! 見た目は難しそうに見えますが 単純な割り算を計算するだけですからね a を移項したいのであれば a で両辺を割る。 そのように考えると混乱しないですよ。 これから分数の移項など少しづつ、ややこしいのが出てきますので、その基本を忘れなければ大丈夫 移項とは、左辺/右辺にある項を反対側へ移動すること。 項を移動するから「移項」と言います。 そして移動する時に「符号を変える」というのがポイントになります。 でも、どうして「符号を変えて移動する」のでしょうか? もはや、当たり前のように移項を使って計算している中学生や高校生は、いざこう聞かれると、 「 分かんないけど機械的にそうやっ
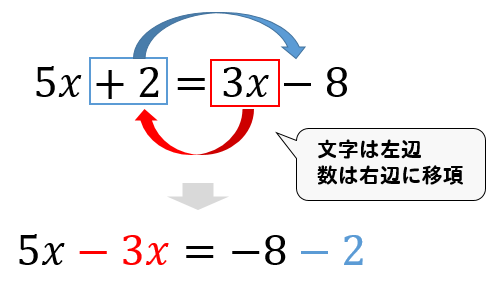
符号を変えて移動した 「ように見える」 。 ⇒ これが「移項」の正体です! おまけ: レベルアップへの"心構え" 中1教科書には、こう書かれています。 等式では、一方の辺にある項を、 符号を変えて他方の辺に移すことができる。 この操作を "移項" という。(1)少数・分数をふくむときは両辺に同じ数をかけて,係数を整数にします。 また,かっこがあったらかっこをはずします。 (2)xの項はすべて左辺に,数の項は右辺に移項します。 移項すると符号が 移項とは 移項とは、左辺にあるものを右辺、右辺にあるものを左辺に動かすということです。ですが、難しい話ではありません。先ほどのルールを思い出せばいいのです。 問:2x+8=4x−12の解を求める。 この時にやってほしいこと。
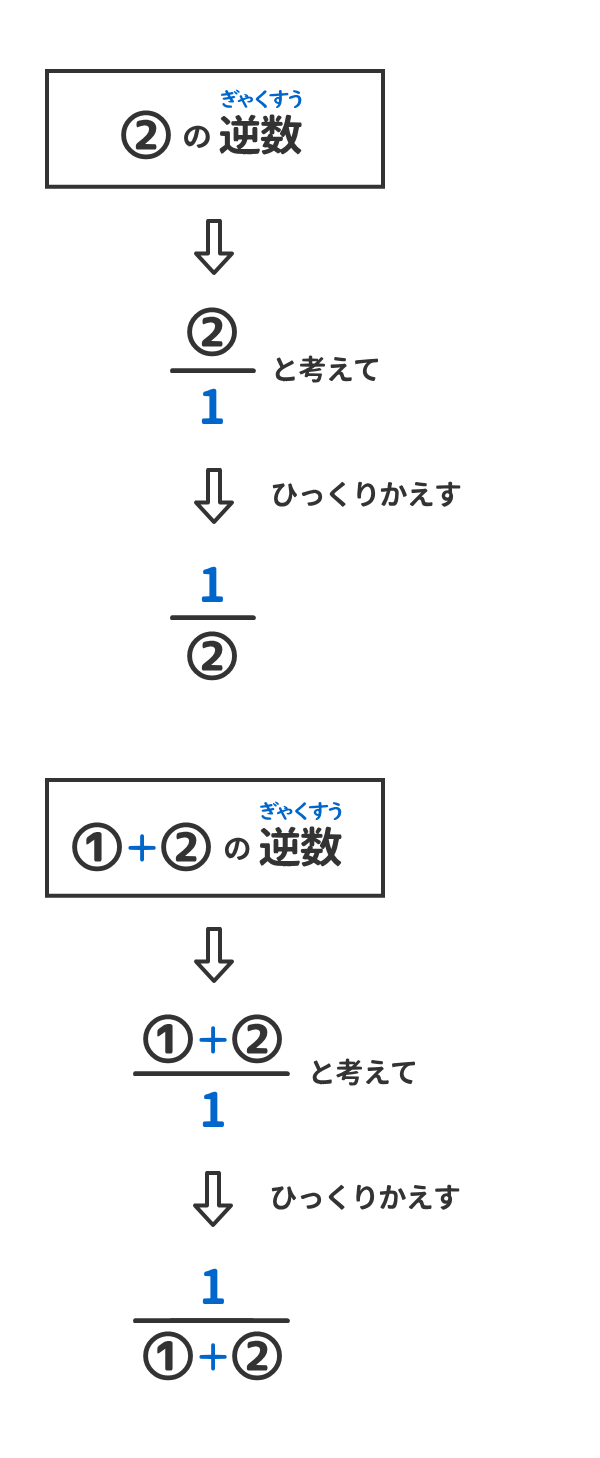
<先 生>まあ、確かに数学よりはスラスラ答えているね。 <かず子>まなぶのこと、ちょっと見直したわ。でも先生、これが指数・対数といったいどんな関係があるんですか。 <先 生>実は、指数と対数の関係もこの英文の書き換えと同じなんだよ。つまり、累乗a M の値がNであるとき、 さて、小学校の算数を思い出してください。分数の割り算は分母と分子をひっくり返すことでかけ算にすることが出来ます。 つまり x÷(1/4) = x×(4/1) = x×4 です。 また「移項」についても思い出しましょう。 x×(1/4) = 2 の両辺に4を掛けて x×(1/4)×4 = 2×4そして,次の手順で考えていけばokです。 手順1 のように指数に−(マイナス)がついているので, を用いて,分数にします。 手順2分母の に着目すると,指数が分数なので, を用いて,分数の指数を の形に直します。 ここでは,分母は, と表すことができるので,



分数の移行についてなんですが例えばxが右辺にあってxが分母にある時と分子にある Yahoo 知恵袋




中一数学 分数を使った方程式 の問題です 絶対間違ってるんで 解き 数学 教えて Goo
(移項という考えも特に意識せず、ただ 「両辺に〇〇」する で進んでください) 左辺の「18+☐」を求めたい「 ☐= の式」にするために 両辺に何をするのか ということです。 同様に とまで、書かせてみてくださいよって、数を右辺に移項します。答えは x4=-5 x=-5-4 x=-9 です。 移項と分数の関係 分数の項があるとややこしく感じますが、移項の方法は同じです。下記の方程式を解きましょう。 です。 なお、下式のケースは移項とはいいません。 まとめ移項 移項とは 一方の辺の項を符号を変えて他方に移動することである。 詳しく 等式の性質を用いて方程式を解く(復習) 6x = 8 5x 6x5x = 8 5x5x 右辺の5xをなくすため 両辺に5xする x = 8 このときに右辺の計算を省略した途中式を書くと
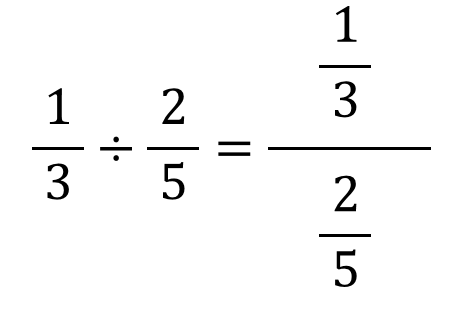



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




中1 数学 方程式6 カッコ 分数 小数 8分 Youtube
移項 前回学習した超重要事項、等式の変形ですが、 この式操作から、「移項」という重要計算技術を得ます。 具体例で見ていきましょう。 \(x8=12\) これを等式の変形を用いて解きます。 4つの等式が並んでいましたが、 (2)分数式は通分する 分数の前の符号がのとき、分子の符号に注意 (3)わり算(除法)は、分数にして約分 (4)分数のわり算は、横の文字を上にのせたあと、逆数にしてかける 3、「式の値」は、計算をしてから、代入する 式の計算を先に 代入するとき、 移項は符号が変わるだけなので、逆数にならない。 ※ (2/3)x=1のとき、x=1× (3/2)というように 逆数ですが、これは移項とは言いません。 x (2/3)=1のとき、x=1 (2/3)と符号を変えるだけが移項です。 5人 がナイス!




中学数学2年 等式の性質と等式の変形 移項 文字について解く 受験の月



分数の移行がわからないので 教えてほしいのですが 正弦定理の公式に当ては Yahoo 知恵袋
電験三種の計算問題では、「等式変形」が頻繁に登場する。 この「等式変形」なるものがスムーズにできないと、計算問題を解くことができないし、過去問題の解説を理解することもできません。 いわゆる「詰んだ」状態になってしまうのです。 この記事は中学生・高校生のときに学ん ジャマな4 x を右辺に移項 $$3y=124x$$ y にくっついている3を割り算で右辺に持っていく $$y=(124x)\div3$$ $$y=\frac{124x}{3}$$ これで完成です! 分数が2個ある場合には 分母にある数の最小公倍数を掛けて分数を消してやりましょう。方程式 (移項)_例題と練習 一方の辺の項を符号を変えて他方に移動すること。 ① 数字の項を右辺に,xを含む項を左辺に移項する。 ② ax = bの形にする。 ③ 両辺をxの係数で割る。
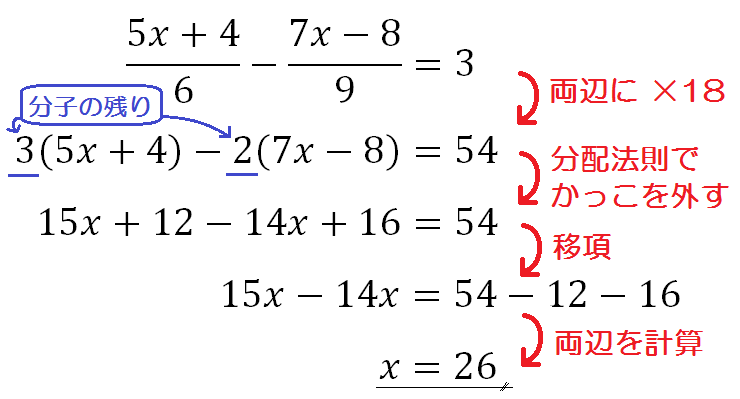



中1 1次方程式 でつまずく原因と解決法 分数
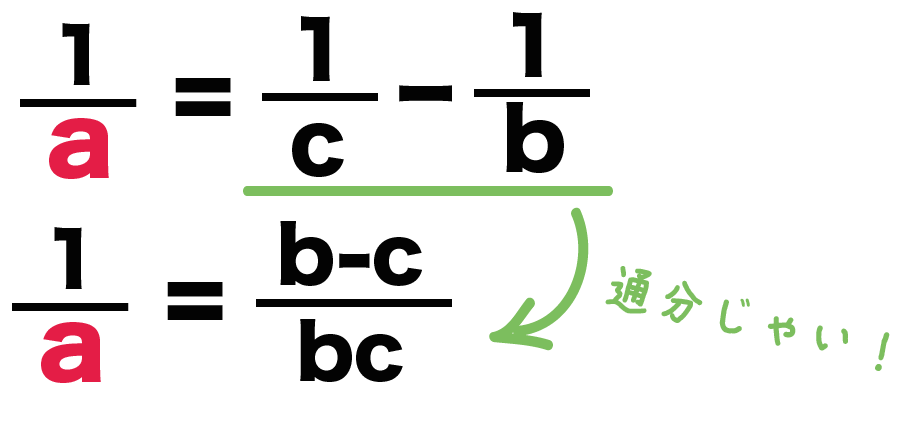



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく
③のようにxの係数が分数になると間違えやすくなります。 その際は分母と同じ数を両辺にかけて、分数をなくしてから計算を進めましょう。 移項とは? さて、例2①の問題と解答を、もう一度見てください。 ①x+5=23 x+5-5=23-5 分数を含む項では、分子から文字をいったんおろして考えてください。 先ほどの でいえば としてやります。すると、 となります。よーーく見てみると が文字xの前にあることに気づきますよね?? つまり、 の係数は「 」なのです。見た目に惑わされない 最高 50 分数 の 移項 分数の移行について質問です なぜこの様になるのでしょうか 中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを



みお ノミはアリのマイナス1000倍くらいの大きさ と聞かれたのが発端で 分数とか割り算とか移項の話とかで盛り上がった今日の夕食 T Co 0tvvobbjdl



分数の移行について質問です なぜこの様になるのでしょうか 途 Yahoo 知恵袋
移項 移項とは 一方の辺の項を符号を変えて他方に移動することである。 詳しく 等式の性質を用いて方程式を解く(復習) 6x = 8 5x 6x5x = 8 5x5x 右辺の5xをなくすため 両辺に5xする x = 8 このときに右辺の計算を省略した途中式を書くと 今回は 「分数をふくむ方程式」の解き方がよくわからないという中学生 に向けて、詳しく解説しています。 ・この記事では、次の3つの内容を詳しく説明しています。 ① 分数をふくむ方程式の解き方 (1) ② 分数 をふくむ方程式の解き方 (2) ③ 分数をふくむ方程式の練習問題 なお以前の記事で解説した 「等式の性質」 と 「移項を使った方程式の解き方」 の理解を分母の有理化(3項) 分母を有理化する必要があるのは,分母が a \sqrt{a} a や a b p ab\sqrt{p} a b p など項の数が1つか2つであることが多いです。 その場合は簡単に有理化できます。→分母の有理化や実数化を行う理由




等式変形 について解く は 移項に注意 あんず学習塾のメモ 図表置き場
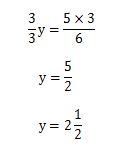



倍分 変形 移項 もう一度やり直しの算数 数学
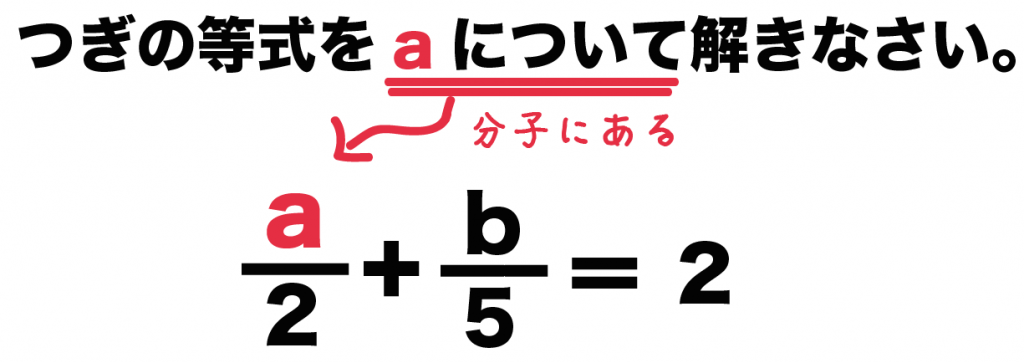
分数が邪魔なので、まずは分数を消してしまいましょう。 4と6を消すためには、最小公倍数である12をかける必要がありますね。 なので分数が2と3なら6倍、2と7なら14倍のようにまず最小公倍数をかけましょう、 かけ算をおこなうと、このような式になります。 そしてこれから「aについて解く」わけですから2bを右に移項する必要があります。多項式・有理式 多項式 とは、変数の整数次の多数の項で表される式のことである。 有理式とは、分数形式で表される式で分母と分子が多項式で表現されるものである。ゆえに多項式は、分母が1の時の有理式であると言うこともできる。ここでは、多項式の形式変換、分解、係数分離などを
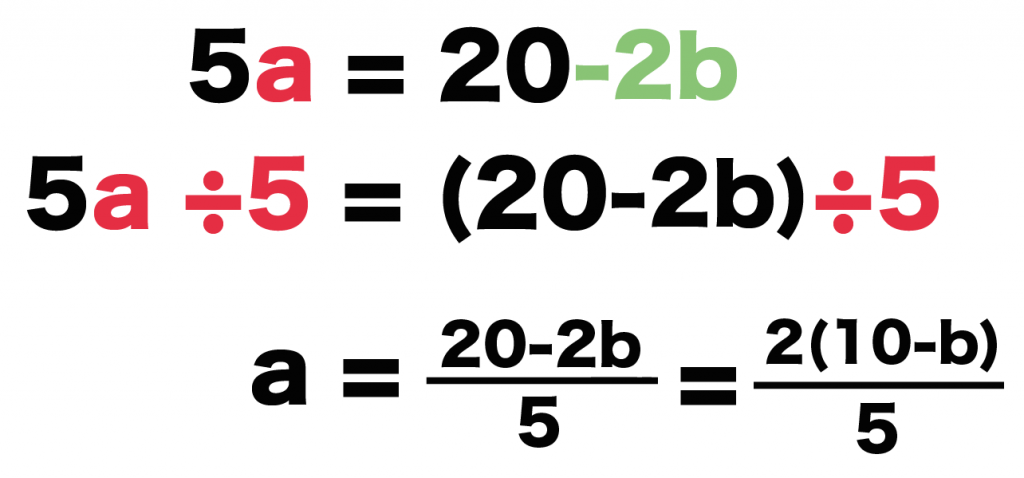



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




等式変形 について解く は 移項に注意 あんず学習塾のメモ 図表置き場




マイナスの指数を移項 ある問題集の設問にて マイナスの指数を分数の 警察官 消防士 教えて Goo




一次方程式 移項を使う問題の解き方と文章題のコツ リョースケ大学




積分定数 超算数 移項る 等式の性質 まず こういう易しいものから 両辺にxがあるような複雑なものまでずらーと並べてから 解ける問題をとりあえず解いて 解けない問題も 大体この附近 分数になりそうだが 整数で挟むとこれよりは大きくてこれ



一次方程式の分数の問題の解き方 中学1年数学 一次方程式
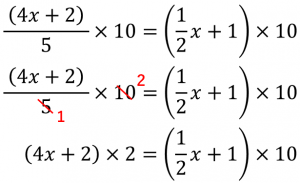



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす
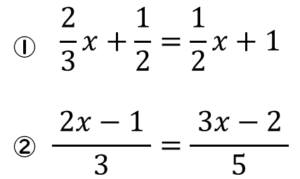



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす



移項とは 1分でわかる意味 やり方 符号 ルール 分数との関係



1




写真を見てください 分数についてです Clear




中1 1次方程式 でつまずく原因と解決法 分数
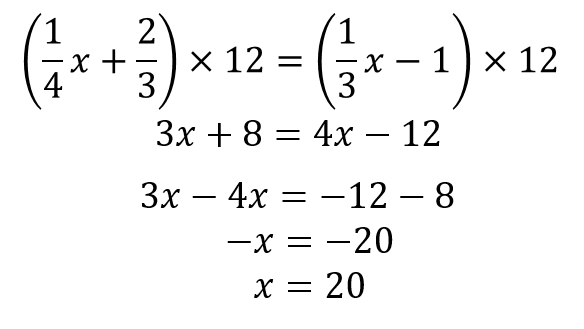



中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ



方程式の解法手順 7パターン デジタル教科書 電子教科書



分数を移行したらどうなるんでしょうか 問題の回答を見 Yahoo 知恵袋




方程式 分母にxがあるときの解き方は 数スタ
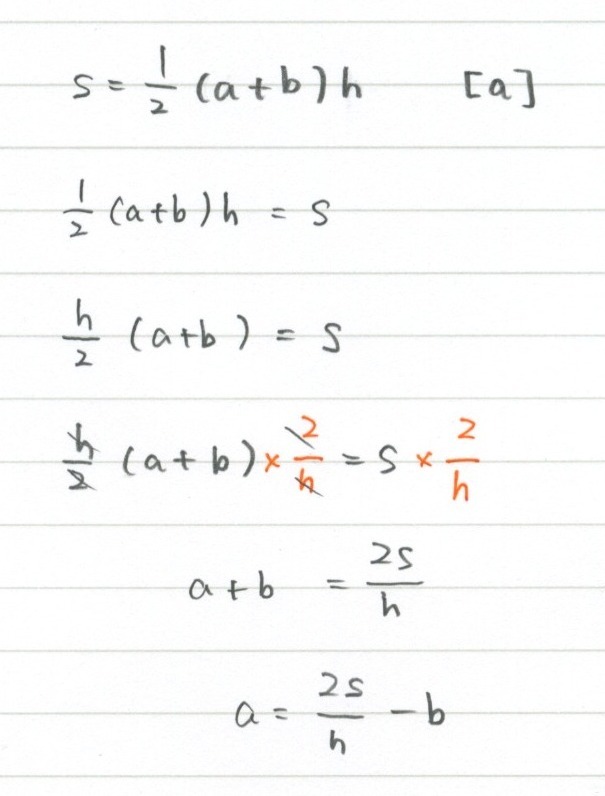



4 6 式の計算 等式の変形 勉強できようサイト
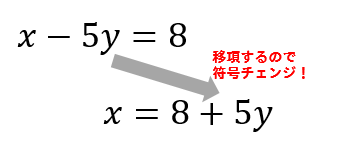



等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ




分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ



方程式の解法手順 係数が分数の形 1 デジタル教科書 電子教科書




方程式の教え方




移項の意味 問題で を飛び越えたら と を逆にしよう 中学や高校の数学の計算問題




分数を使った等式の変形の解き方 成績プラス




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト



分数の式変形 優技録




4 6 式の計算 等式の変形 勉強できようサイト




答えが 6 なんですが 分数になってしまいます 教えてください Clear



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策




方程式 分母にxがあるときの解き方を解説 Youtube




高校数学 不等式の解き方3 分数 小数 練習編 映像授業のtry It トライイット




わかりやすく説明してください お願いします Clear




54 5x 37 3x 4 Dfracx 23 Descubre Como Resolverlo En Qanda




中1 1次方程式 でつまずく原因と解決法 分数



方程式の移項のナゾを解いてみよう 算数 数学 英語塾のフェルマータ
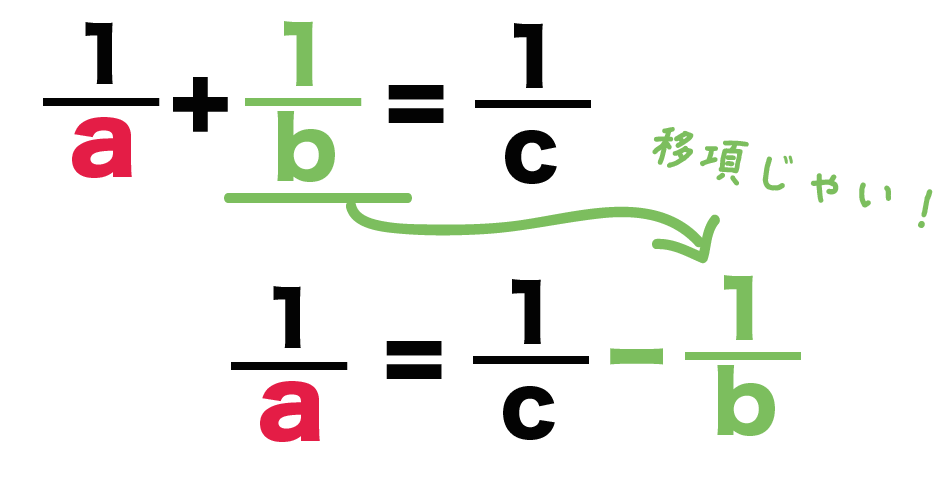



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




計算の仕方がわかりません なぜルート3は移行したら上につくのですか Clear



Math 超簡単 2次方程式を平方完成で解く 働きアリ The 2nd




たけのこ塾 中学数学 等式の変形 のチェックテストです 等式変形 解くポイント 他の項は移項 係数の逆数を両辺にかける 分数では分母の数を両辺にかける 式にかけられている数の逆数を両辺にかける の画像でチャレンジし
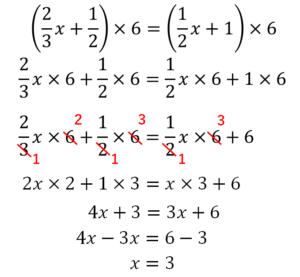



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす



分数は移項すると必ず逆数になるのか 移項は符号が変わるだ Yahoo 知恵袋
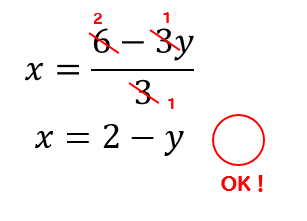



等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ




方程式の教え方
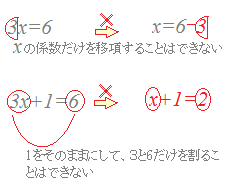



1次方程式の解き方




一次方程式 移項を使う問題の解き方と文章題のコツ リョースケ大学



分数は移項すると必ず逆数になるのか 移項は符号が変わるだ Yahoo 知恵袋



方程式の移項のナゾを解いてみよう 算数 数学 英語塾のフェルマータ




中1 1次方程式 でつまずく原因と解決法 分数




一次方程式の解の求め方 数学fun




中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト



等式 の変形をして必要な情報を取り出そう 電験3種web



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす




中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく
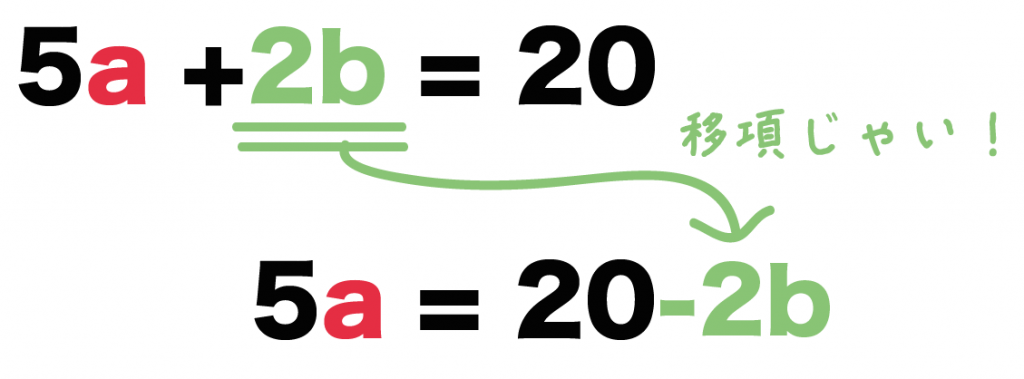



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




分数の計算 X 100 5 恥ずかしながら分数の計算を忘れてしまい 数学 教えて Goo



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




中一数学13方程式 小数 分数 計算を楽にしたいなら必ずみて ニコニコ動画



一次方程式の分数の解き方 やさしく解説



分母をはらう



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




連立方程式 分母の数が大きい場合の計算 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




中一数学 分数を使った方程式 の問題です 絶対間違ってるんで 解き 数学 教えて Goo




ベストコレクション 分数 の 移項 ニスヌーピー 壁紙



普通の整数を移項すると分母になるのに 分数の分子を移項したら分子 Yahoo 知恵袋



1




中学数学 方程式 50 方程式を解く 分数の混じったもの Youtube



数学について質問です何故3分の1を移項すると3になるのかが分かりません Yahoo 知恵袋




積分定数 超算数 移項る 等式の性質 まず こういう易しいものから 両辺にxがあるような複雑なものまでずらーと並べてから 解ける問題をとりあえず解いて 解けない問題も 大体この附近 分数になりそうだが 整数で挟むとこれよりは大きくてこれ




移項で方程式を解く 中学数学 方程式 2 Youtube



両辺とは 1分でわかる意味 両辺の二乗 両辺を割る 分数との関係
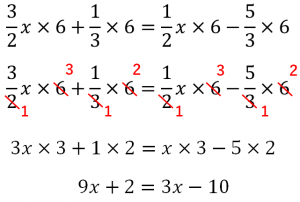



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす




高校数学 不等式の解き方3 分数 小数 練習編 映像授業のtry It トライイット




等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ
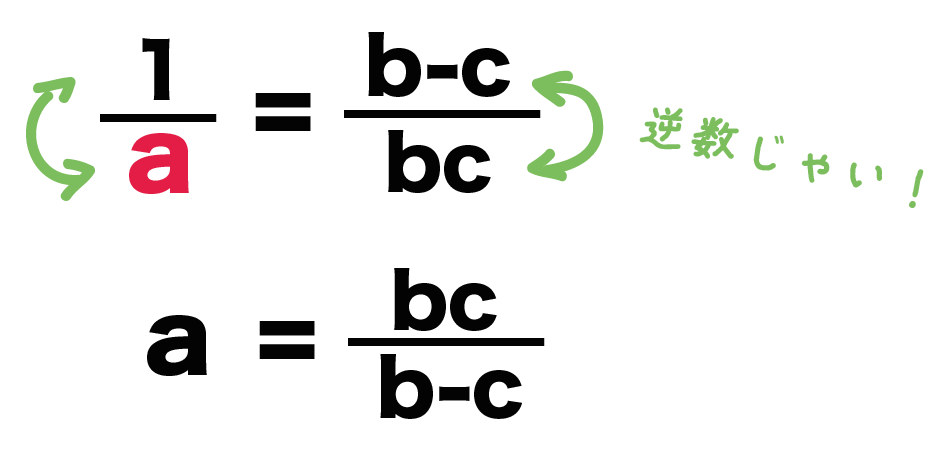



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




写真を見てください 分数についてです Clear




中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく




等式の変形で 解き方を説明してくれませんか 分数などが含まれている等式が苦手です Clear




数学 移項のやり方がよく分からなくなった時のコツ



Q Tbn And9gctk Swttxlrvv51apkcruiezqziseion0acgnekykfmfrjsyspu Usqp Cau



一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト
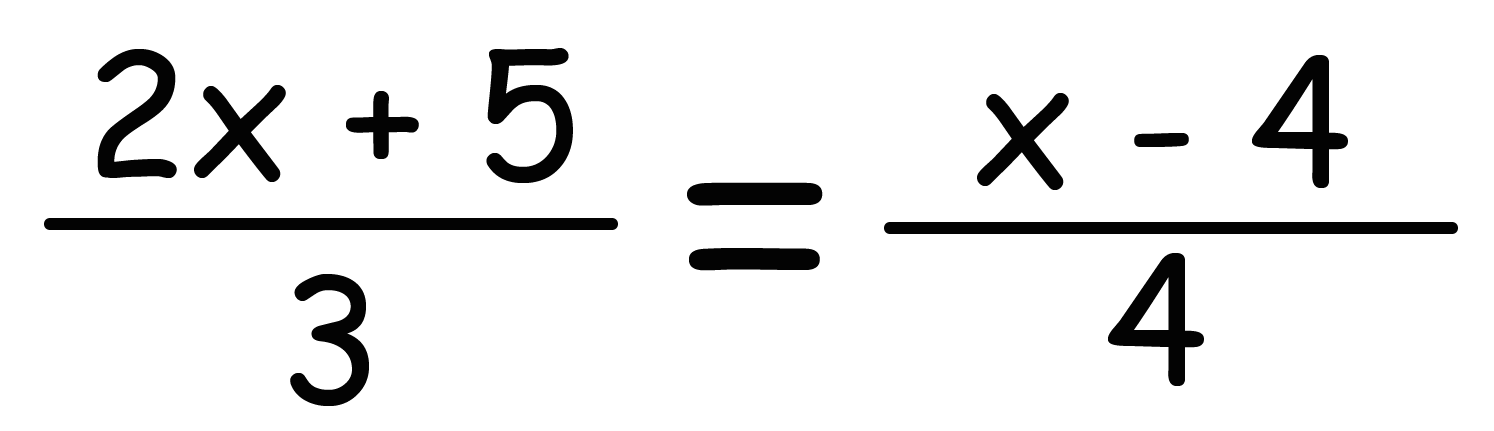



中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく




中1 1次方程式 でつまずく原因と解決法 分数
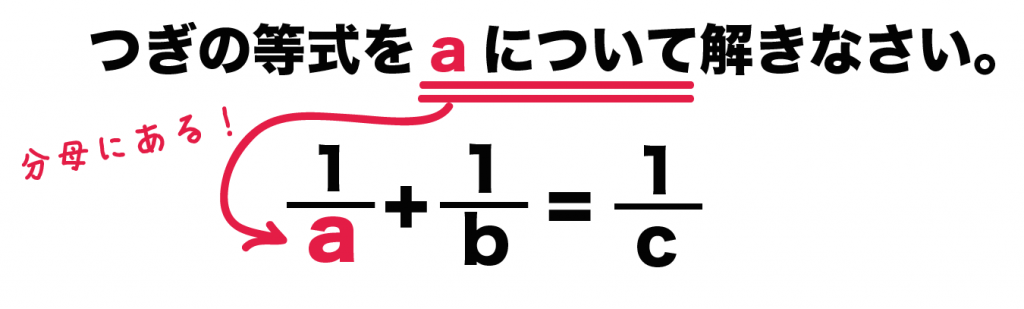



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




方程式 効率良い復習 テクニックで勉強 テストが楽しくなるブログ



方程式の移項のナゾを解いてみよう 算数 数学 英語塾のフェルマータ
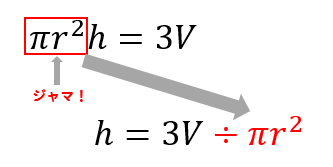



等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ



分数の移行がわからないので 教えてほしいのですが 正弦定理の公式に当ては Yahoo 知恵袋



分数は移項すると必ず逆数になるのか 移項は符号が変わるだ Yahoo 知恵袋



Q Tbn And9gcqejritz309hy5ccak9mag9yi71ab0izpynx1adu6tlmgkqk3rw Usqp Cau



移項とは 1分でわかる意味 やり方 符号 ルール 分数との関係




方程式 効率良い復習 テクニックで勉強 テストが楽しくなるブログ



両辺とは 1分でわかる意味 両辺の二乗 両辺を割る 分数との関係



0 件のコメント:
コメントを投稿