三角形 の 相似 777356-相似 の 三角形 条件

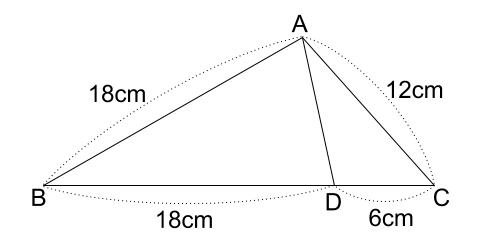
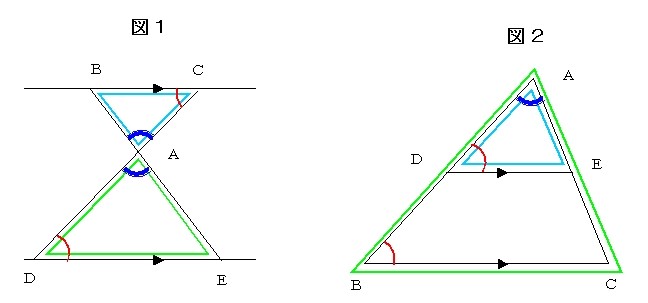
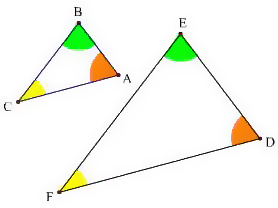
相似な三角形から面積比を考える まずは基準となっている oadの面積をsとして考えていきます。 この台形の中から相似な三角形を探していくと 対頂角や錯角が等しくなることからと DE= 12 cm;相似三角形 如果两个三角形只是大小不同（也可能要把其中一个翻转或旋转），那么它们便是 相似 的。 这些三角形都是相似的： （相等的角用同个数的弧线标记） 它们有些是大小不同的，也有些是旋转或翻转了的。 两个相似三角形： 所有的对应角

三角形の相似条件 イ弋マ本ゼミナール

相似 の 三角形 条件

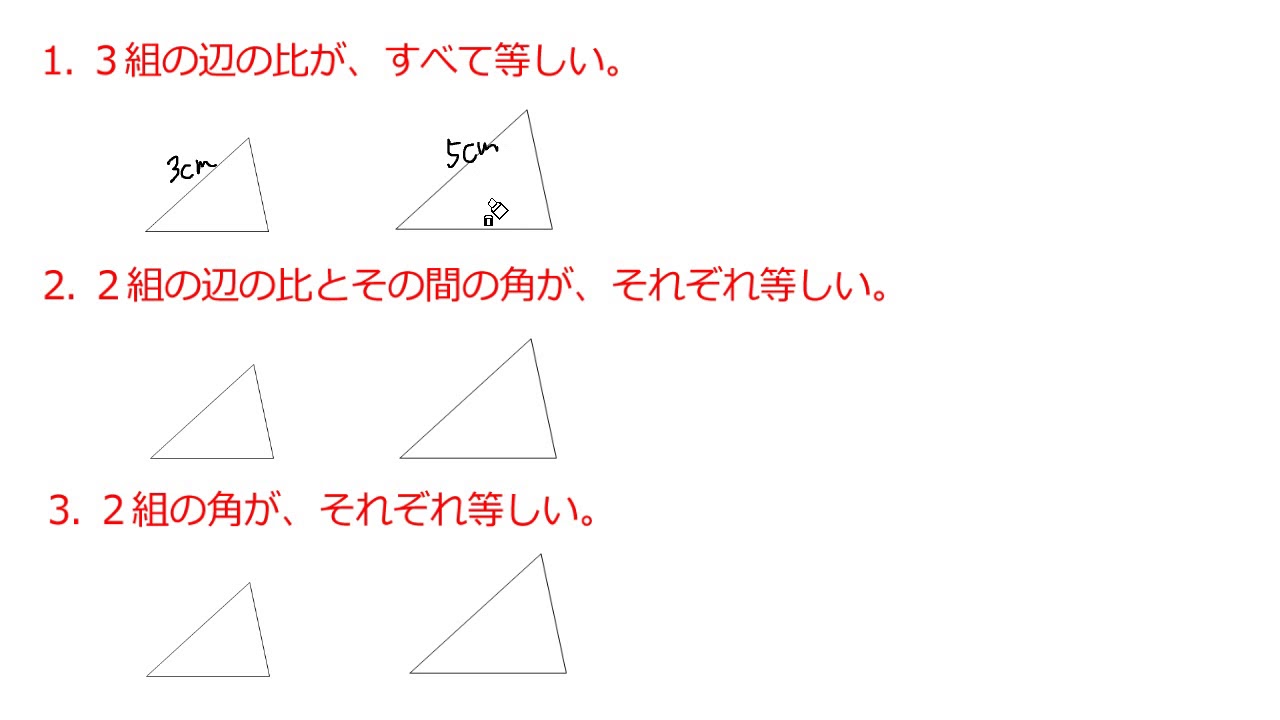
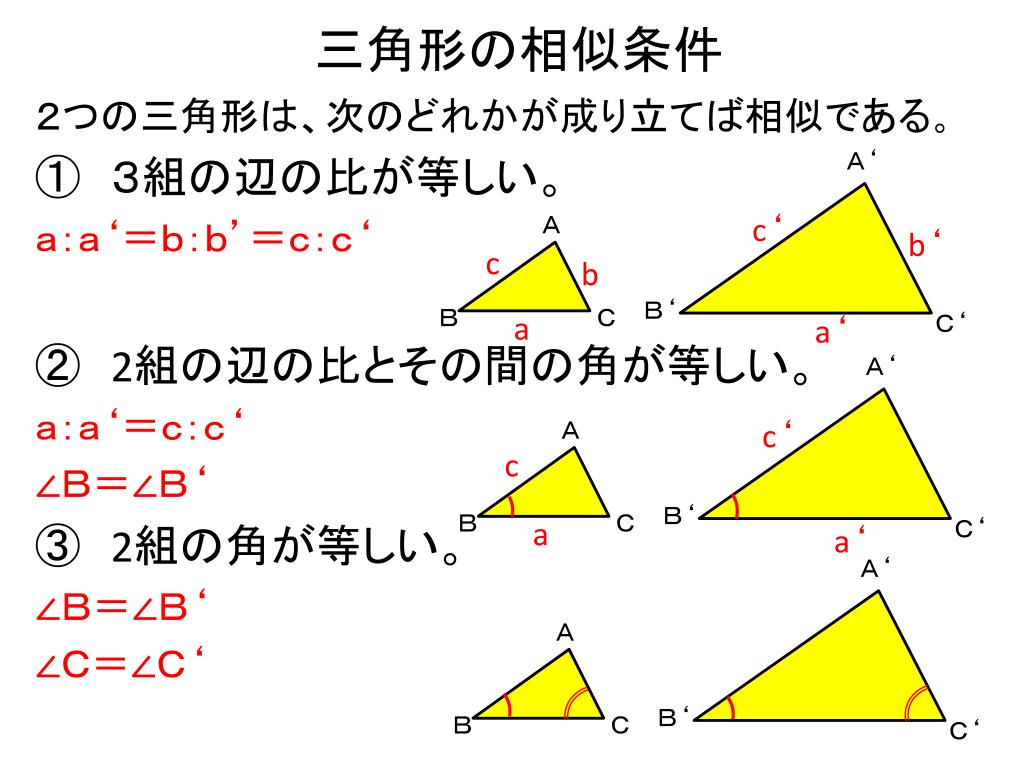
相似 の 三角形 条件-三角形の相似条件 三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき 3 2組の角が、それぞれ等しいQ1 三角形の相似条件として、正しくないものを選びましょう。 3組の辺の比がそれぞれ等しい。 2組の辺の長さとその間の角が

三角形の相似 合同条件 優技録

 · 相似三角形(similar triangles)是指三角分别相等，三边成比例的两个三角形。 相似三角形是几何中重要的证明模型之一，是全等三角形的推广。全等三角形可以被理解为相似比为1的相似三角形。相似三角形其实是一套定理的集合，它主要描述了在相似三角形是几何中两个三角形中，边、角的关系。 · 九年级数学直角三角形相似的判定ppt,直角三角形相似的判定 第三课时 执教者：邓玉春 已经学习的三角形全等的判定定理有： aas asa sas sss hl 已经学习的三角形相似的判定定理有： 两角对应相等，两三角形相似。 两边对应成比例且夹角相等，两三角形相似。DF = 14 cm;

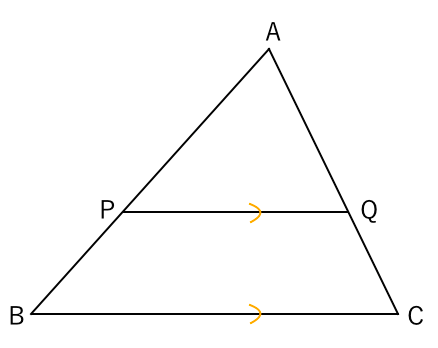
 · 直角三角形の中に正方形が入った問題は相似の三角形を作って解く 相似＋三角形のテクニック3つ!の中学入試問題等 問題）浅野中学（問題文はワイが簡略化してます） 2つは同じ三角形です。defgは正方形です。正方形の1辺の長さは？三角形の相似条件より相似な図形を選ぶ あてはまる相似条件を選ぶ また、その相似条件をいいなさい。 (頂点は，対応する順にあわせて書くこと。) 問2．下の図の三角形を、相似な三角形の組に分けなさい。 また、相似比と相似条件をいいなさい。一、平行线截比例线段定理 设 ADE 为任何三角形，而线段BC 平行于 DE，则 AB/BD = AC/CE 要证明这个定理，画线段BF 平行于 AE 来形成平行四边形BCEF： 三角形 ABC 和 BDF 有相等的角，所以是相似三

/05/ · 複素平面での三角形の相似 点 P(z1),Q(z2),R(z3),P′(w1),Q′(w2),R′(w3) P (z 1), Q (z 2), R (z 3), P ′ (w 1), Q ′ (w 2), R ′ (w 3) に対し · 三角形の相似条件 三角形の相似を証明するためには、「相似条件」というものを使います。 相似条件には、以下の \(3\) つがあります。 相似条件①3 組の辺の比がそれぞれ等しい \(3\) 辺の比がそれぞれ等しければ、相似と言えます。AC = 7 cm;

中学数学 相似の証明 その１ 中学数学の無料オンライン学習サイトchu Su

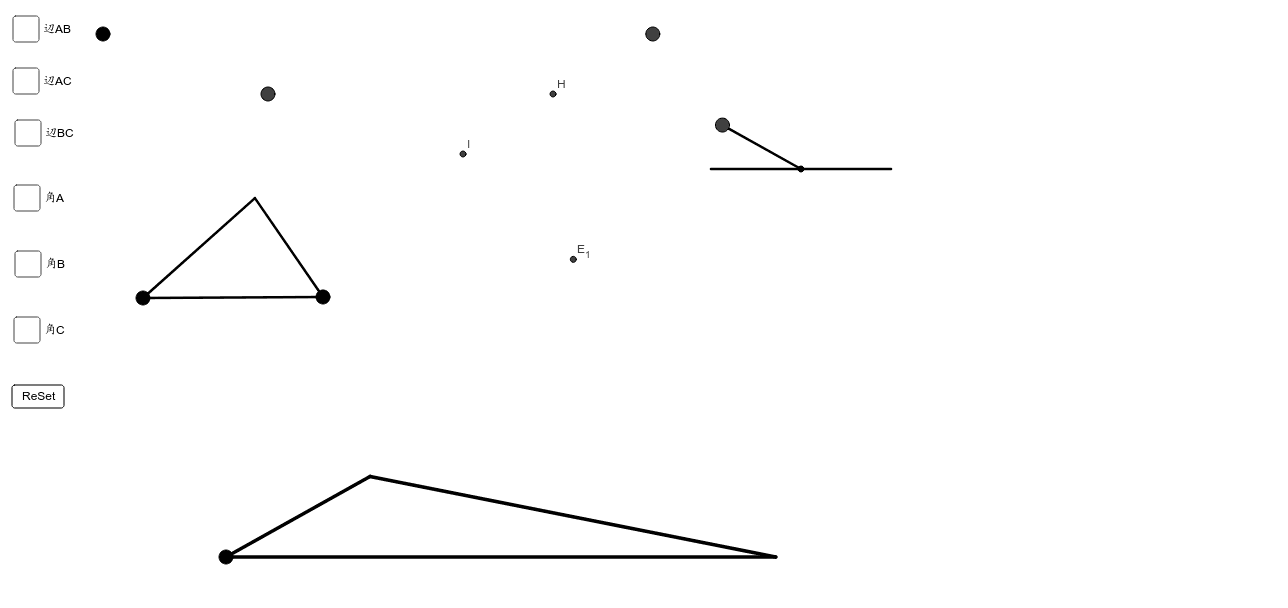
三角形の相似条件的副本 Geogebra

 · 1、锐角三角形：三角形的三个内角中最大角小于90度。 2、直角三角形：三角形的三个内角中最大角等于90度。 3、钝角三角形：三角形的三个内角中最大角大于90度，小于180度。 其中锐角三角形和钝角三角形统称为斜三角形。EF = 16 cm;若兩個三角形相似，則三個 對應角相等 。 若2個三角形相似，則三個 對應邊長成比例 。

1

かみのドリル 三角形の相似のドリル 中受

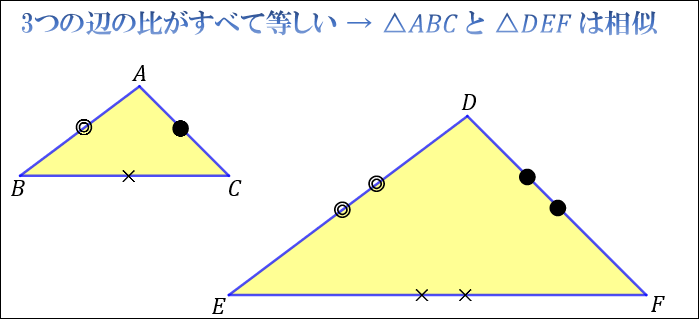
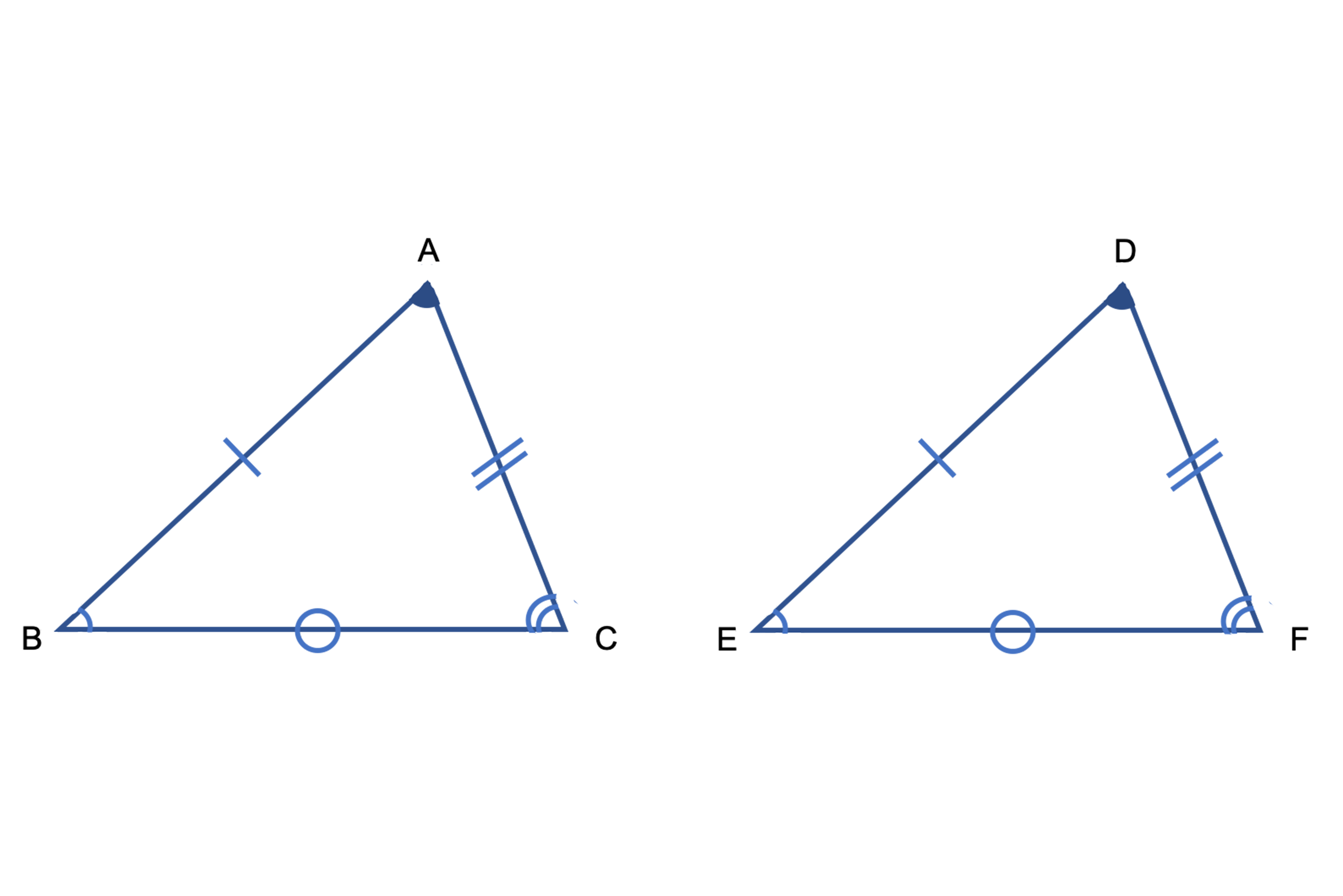
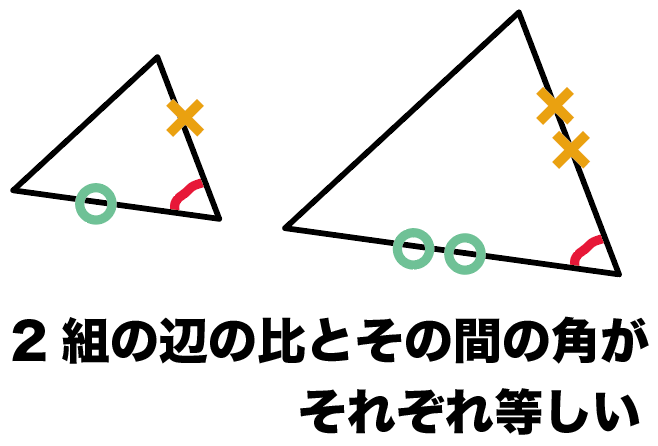
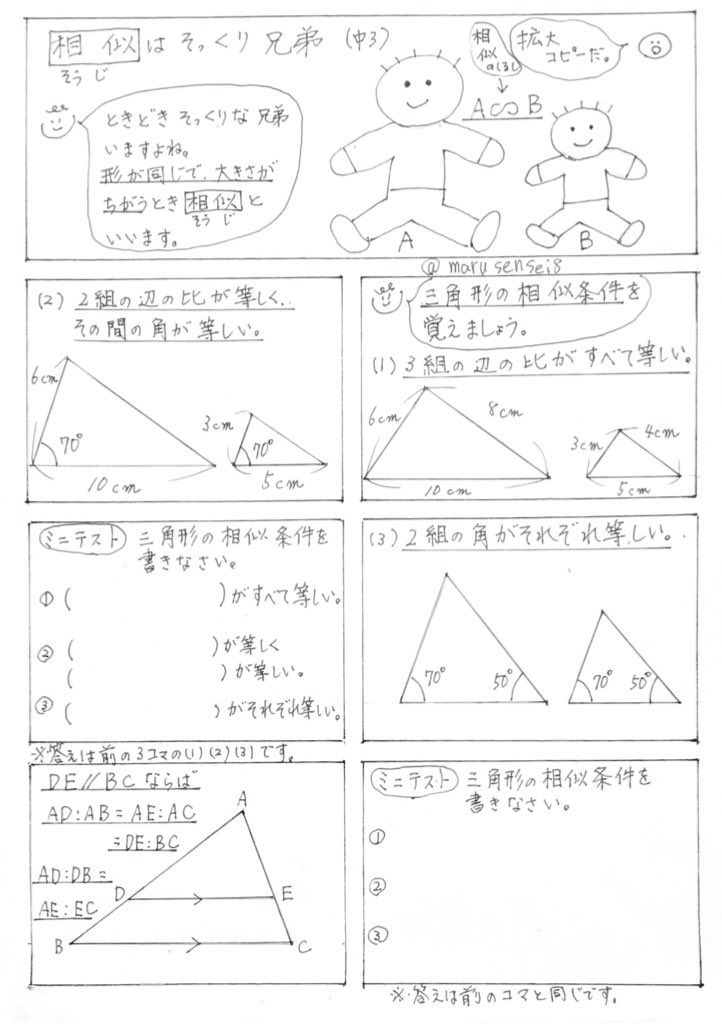
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru · 1 相似三角形的判定定理 (1)平行于三角形一边的直线和其他两边 (或两边的延长线)相交，所构成的三角形与原三角形相似； (2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似； (简叙为：两边对应成比例且 · 相似条件 ・3組の辺の比がすべて等しい （例ac：df＝cb：fe= ba：ed） ・2つの角が等しい (例 ∠abc=∠def、∠acb=∠dfe) ※例は上の画像の三角形abc・defにならって記述 相似になる条件を上にまとめました。

相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学

高校入試 英語 数学 図形と相似 三角形の相似証明

三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件を確認していき · 三角形の相似 相似とは2つの図形の片方を縮小・拡大して、平行移動、回転移動、対称移動を行えばもう片方の図形と重なる関係のことを言います。 つまり、 2つの図形の形が同じであれば相似 であるといえます。 大きさや、向き、鏡のように反転していても相似は成り立ちます。 三角形に限らず、四角形でも円でも相似は成り立ちますが、試験や入試で問われる · 相似三角形的判定定理及性质 05 文/张敏

三角形の相似条件 ドリるーむ

三角形の相似条件 イ弋マ本ゼミナール

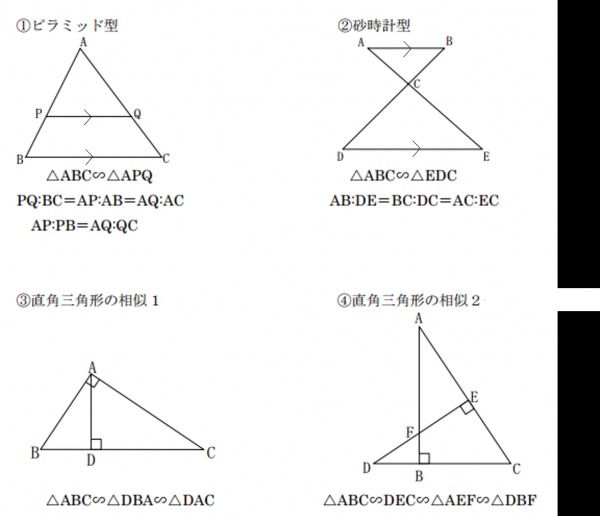
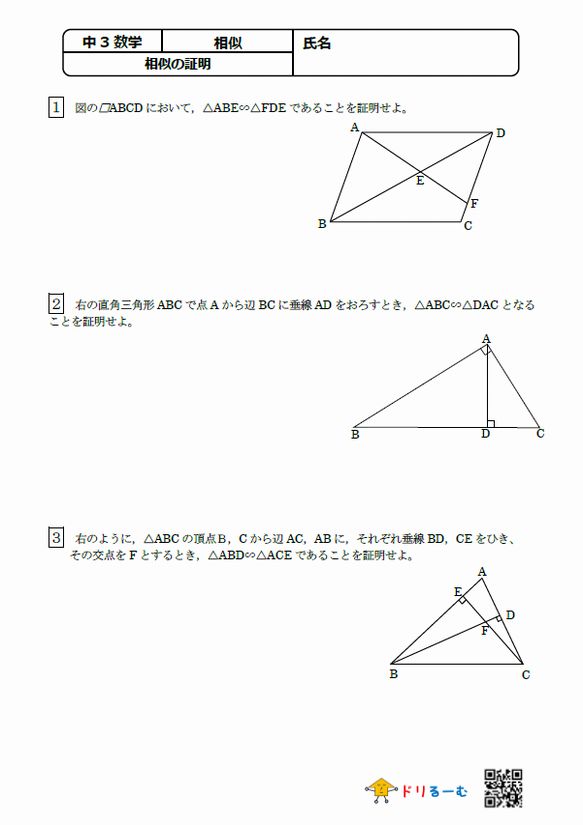
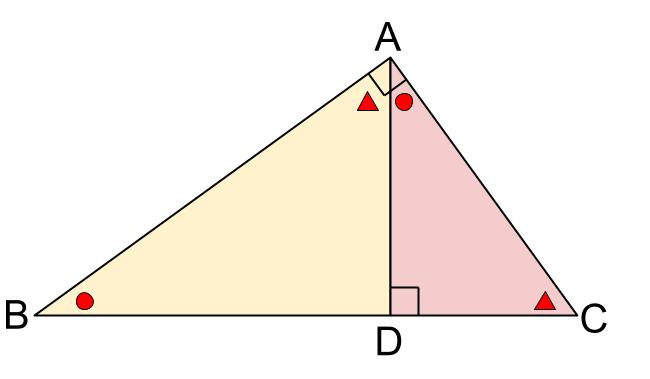
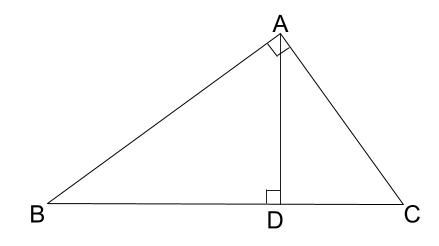
直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います！ 直角である頂点から斜辺へ垂線を静止画 e1soj1jpg 600×400、 1195KB 中学数学 ⇒ 相似と比（中学3年） ⇒ 三角形の相似条件 三辺の比相当 三角形の相似条件の1つを示しています。 2つの三角形は，対応する3組の辺の比がすべて等しいとき，相似になります。 · 直角三角形の相似条件 直角三角形は特殊な三角形なので、相似条件も特殊になっています。 詳しく見ていきましょう!

相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

直角三角形の相似条件 具体例で学ぶ数学

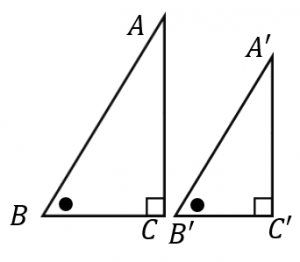
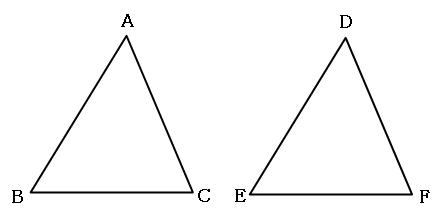
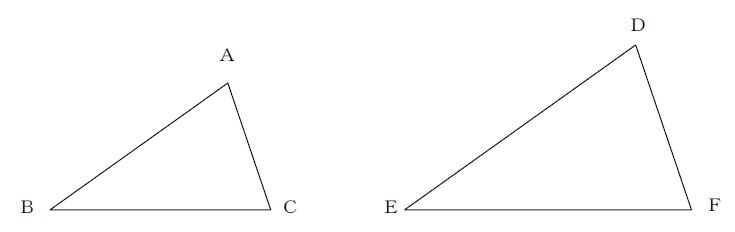
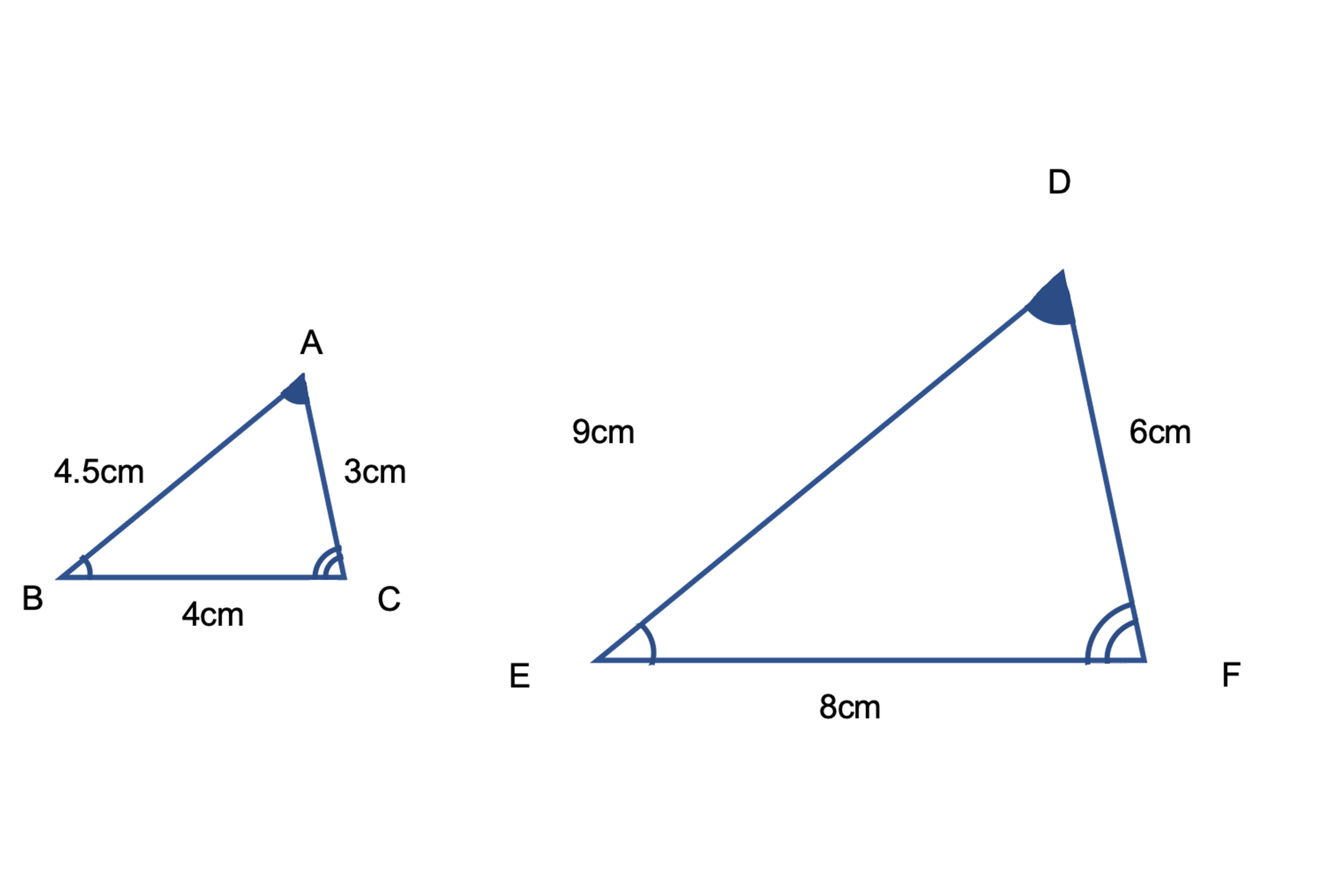
 · 1）相似→三角形ebg7三角形cfg5なので対応する辺fg5bg7の比 2）高さが同じ三角形の面積は底辺の長さの比に比例→三角形BGC「7」：三角形FGC「5」 答え）14と7/12 （ c ㎡と聞かれてるので数字で答える、もちろん「と」はいらない） · 「3つの辺の比」 がすべて等しいとき、2つの三角形は相似って言えるんだ。 たとえば、2つの ABCと DEFを想像してみて。 AB = 6 cm;だ。 この2つの三角形は相似になってるはず。 なぜなら、 AB DE = 6 12 = 12;

三角形の相似条件について 図解で分かる相似条件 アタリマエ

Studydoctor相似比と面積の計算 中学３年数学 Studydoctor

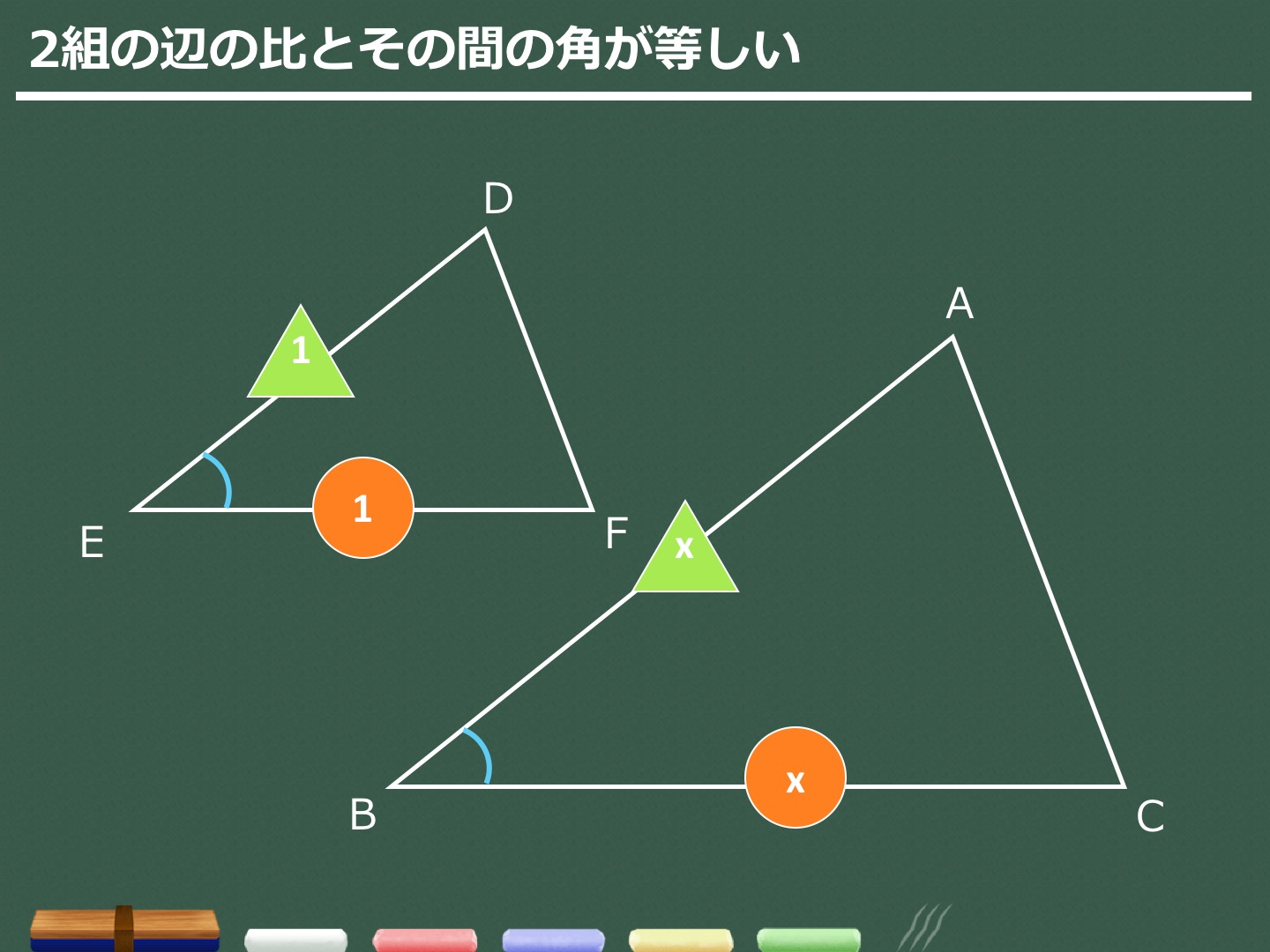
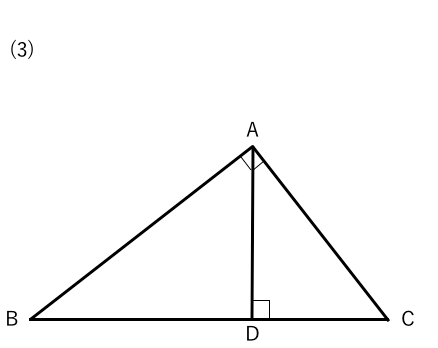
受力分析中的"相似三角形"方法 这里主要讲的是"三力平衡"问题。 分析平衡问题，一般采用的是力的合成或者分解方法，分解又以正交分解为"正统"。 后来，我又跟小伙伴们分享了"拉密定理"，而拉密定理つまり，三角形の相似条件は， 3辺 がそれぞれ等しい→ 3組の辺の比 がすべて等しい 2辺 とその間の角がそれぞれ等しい→ 2組の辺の比 とその間の角がそれぞれ等しい 1辺 とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい となります。 3の■三角形の相似条件 右の (1) (2) (3)は三角形の 相似条件 と呼ばれており，そのうち１つでも成り立てば２つの三角形は 相似 になる． 逆に，２つの三角形が相似であるとき，右の (1) (2) (3)はすべて成り

3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ

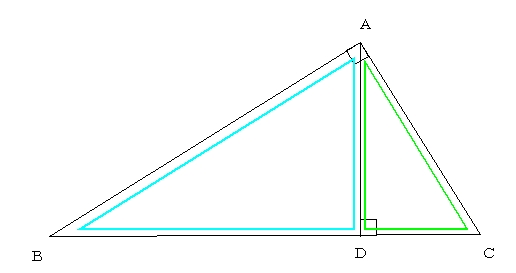
相似 直角三角形

相似三角形を英語に訳すと。英訳。similar triangles 80万項目以上収録、例文・コロケーションが豊富な無料英和和英辞典。 · 三角形相似是初中数学里非常重要的知识点，是中考中一定会涉及的考点之一。 三角形相似的判定和应用题型千变万化，但"万变不离其宗"，常用的一共有以下8种模型。 1、8字形模型 2、反8字形模型 3、A字形模型 4、反A字形模型 5、共边反A字形模型 6この条件で、なぜ2つの三角形が｢相似｣であることが言えるのか、その理由を説明しなさい。 相似③三角形の相似条件d 学 年 3年 学習日： 月 日（ ） 中学校数学 3b5－3d 中学校数学・ワークブック 年 組 氏名

相似な図形 三角形の相似条件 相似比 勉強ナビゲーター

三角形の相似条件

三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。 ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていき · 相似这个知识点，是初三几何知识中的核心，锐角三角函数会用相似，旋转会用到相似，圆中也会用到相似。 全等的知识点很重要吧，相似知识点的重要性不低于全等，为啥呢？ 几乎所有省市的中考题压轴题都是2个，几何゜ 合同変換，相似変換などの意味。 (2) 三角形の相似曵件を明らかにし，合同曵件や相似曵件を用いて， 図形の性質の理解を济める。 ゚ 三角形の相似曵件。 ゜ 平行線および平行平面に関する線分の比についての性質。 ゞ 三角形および平行四辺形の性質。

相似な図形 計算について覚えること 苦手な数学を簡単に

合同とは 相似とは

BC = 8 cm;Similar transformation (相似形の変身) ワークシート okyota Fold the rectangle (長方形の折り返し 相似) ワークシート okyota Fold the rectangle (長方形の折り返し 相似)minor change

中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学

三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

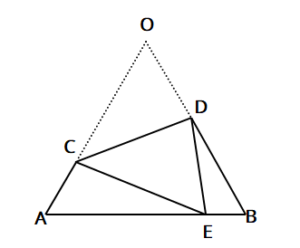
高校入試対策数学 折り返し図形と相似の融合問題 中学生勉強サイトあかね先生

中3数学 相似な図形と相似条件のポイントまとめ Atstudier

相似な図形 相似条件の練習問題 苦手な数学を簡単に

相似図形

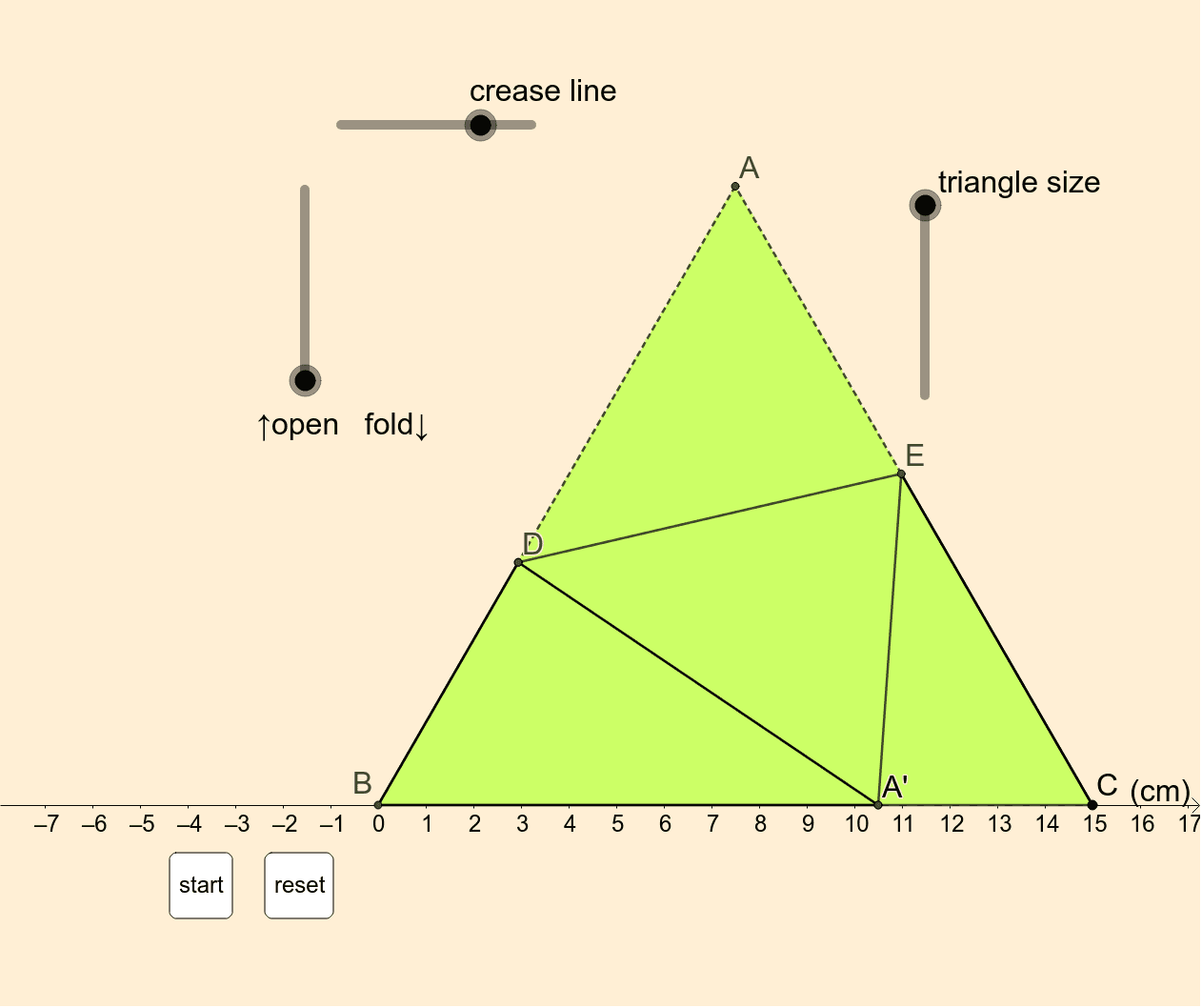
Fold Equilateral Triangle 正三角形の折り返し 相似 Geogebra

５章１節２ 三角形の相似条件２ 数学のすすめ

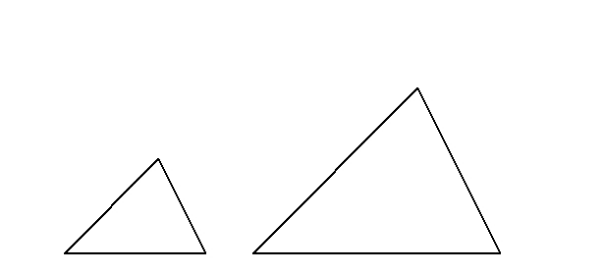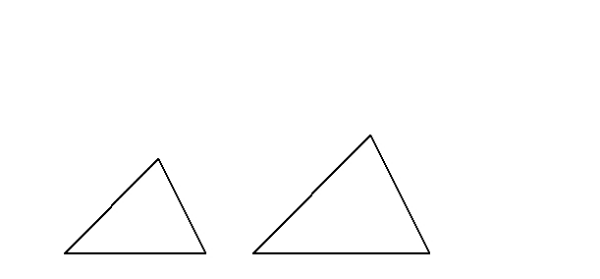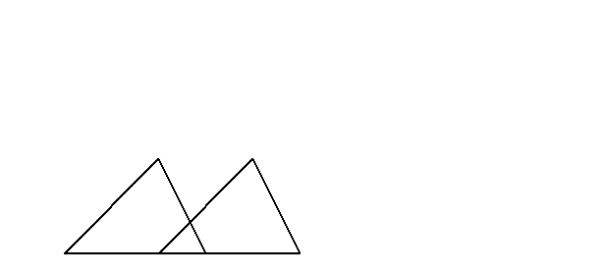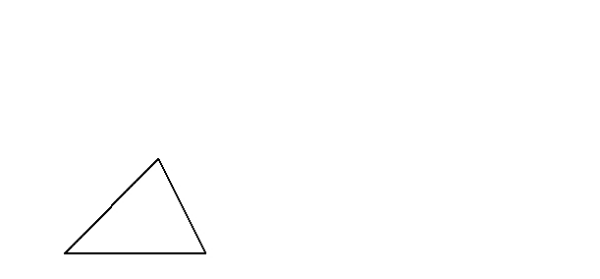
三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学

三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

数学 中3 48 相似の証明チャレンジ Lv 3 Youtube

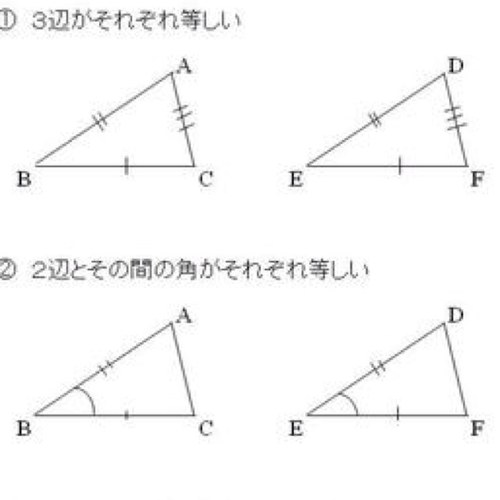
三角形の相似条件bot Triangle Bot Twitter

至急 この問題の相似な三角形と相似条件を教えてください 考え方が分かりません Clear

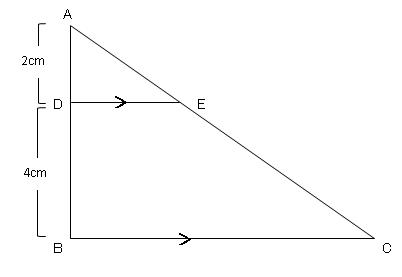
相似と面積比 1 ネット塾

中３数学 相似 直角三角形と相似 Youtube

平面図形の基礎

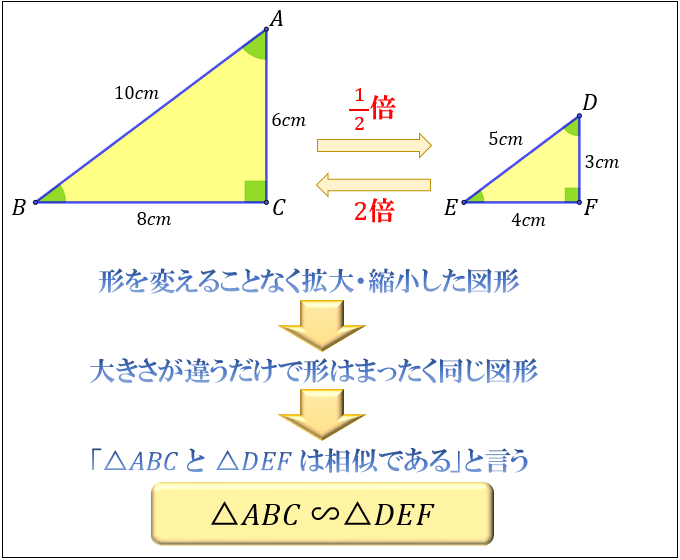
相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ

三角形の相似 合同条件 優技録

相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典

相似な三角形を見つける 修正 Youtube

中3数学 三角形の相似条件２ ２辺の比とその間の角 練習編 映像授業のtry It トライイット

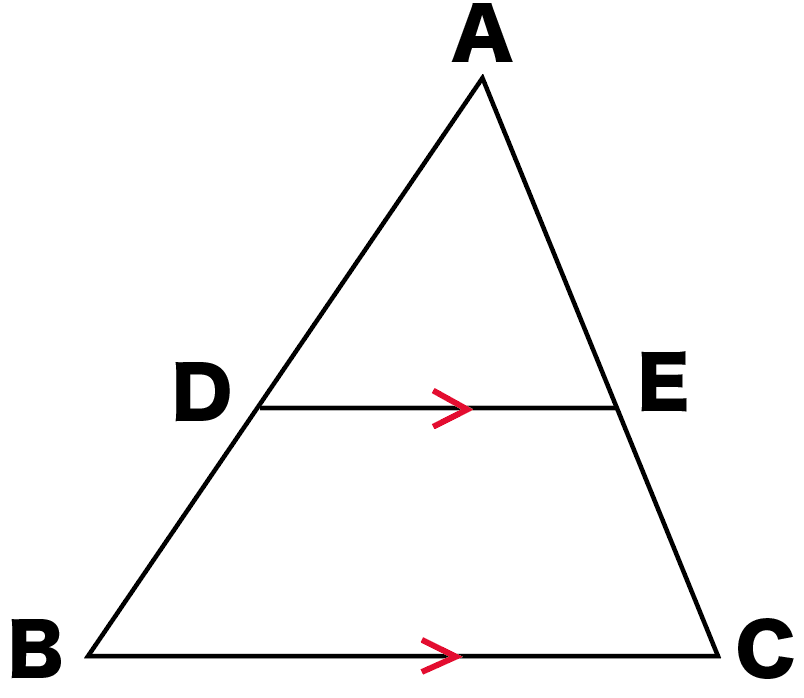
3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく

Math 相似 直角三角形 正三角形と相似 働きアリ

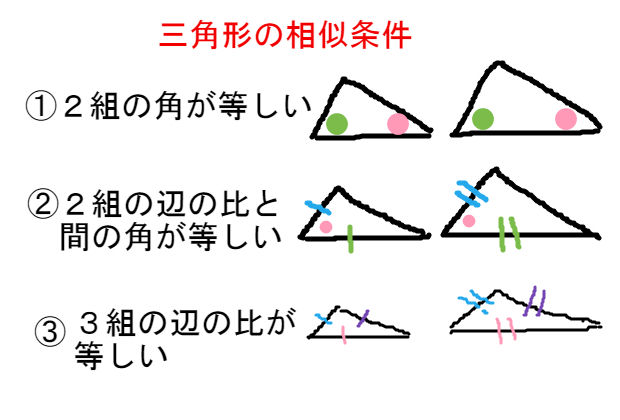
三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト

数学 相似条件と証明 について 下の図 写真 で Abcは Ab Yahoo 知恵袋

三角形の面積比と相似比 チーム エン

Geometry 相似の証明 アメリカの大学で奮闘中

1

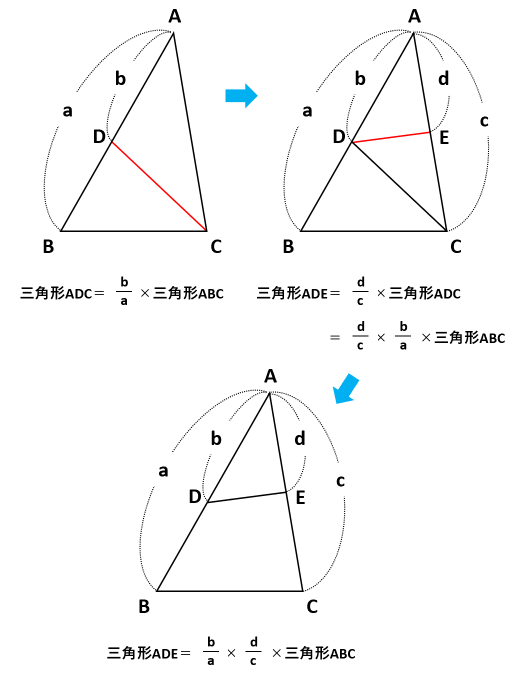
三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ

3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく

相似比とは 1分でわかる意味 面積比 四角形と三角形の問題

相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア

三角形の相似条件と有名な例題３問 具体例で学ぶ数学

相似な図形 Ict教材eboard イーボード

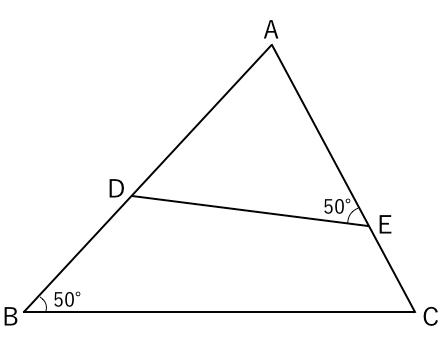
相似 相似な図形を見破れ 苦手な数学を簡単に

高校入試数学 相似な三角形の対策問題

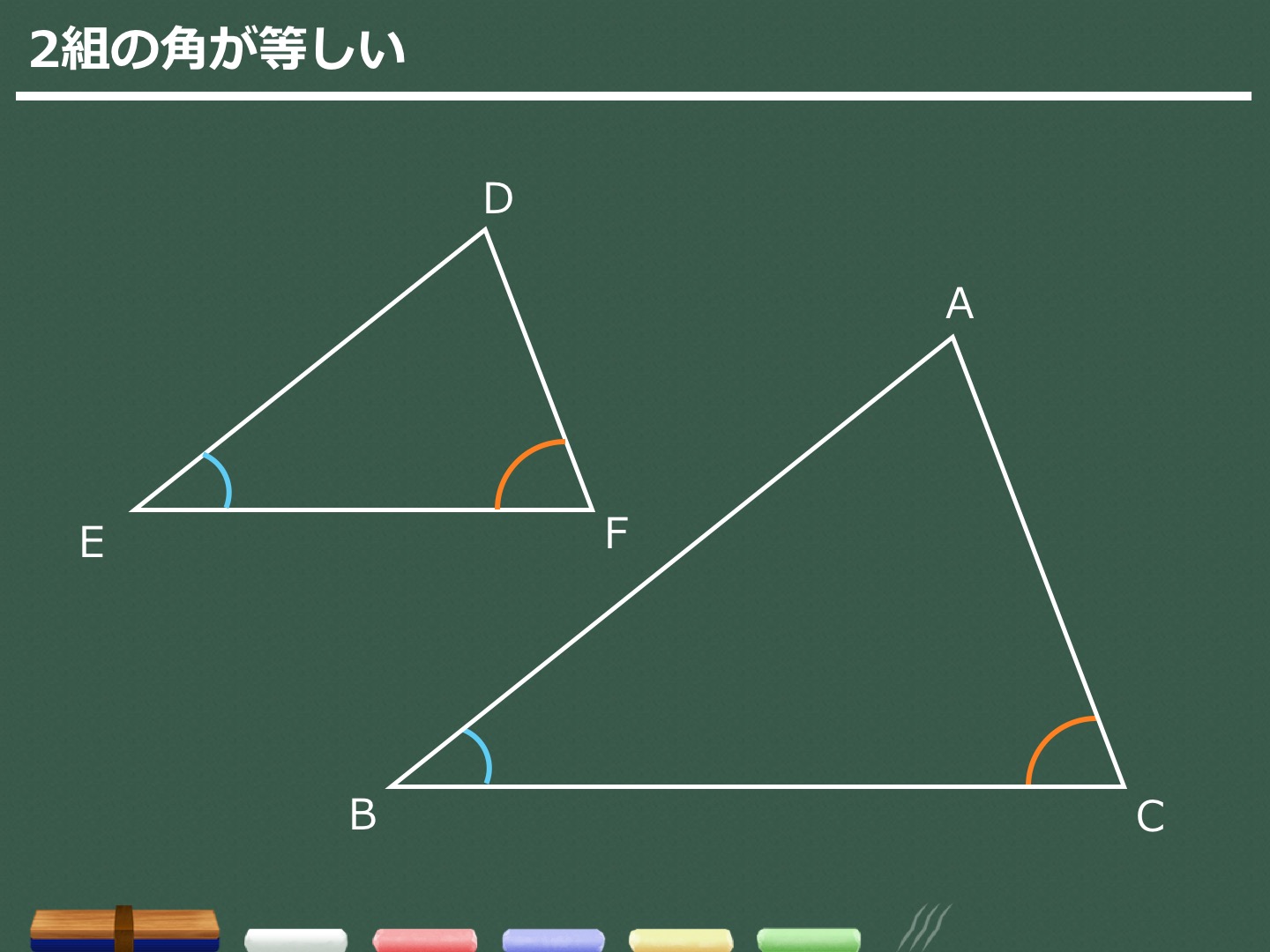
3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ

三角形の面積比を解説 平面図形が苦手でもわかる解き方 基本編 中学受験ナビ

数学 中3 44 三角形の相似条件 Youtube

三角形の相似条件 修正 Youtube

相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし

かみのドリル 相似

相似の証明 2つの正三角形と共通な角 勉強ナビゲーター

三角形の相似条件

記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス

記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス

中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su

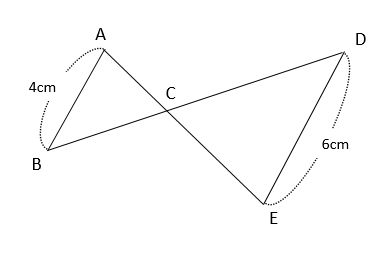
相似 平行線と三角形の問題ではちょうちょかピラミッドを探せ みみずく戦略室

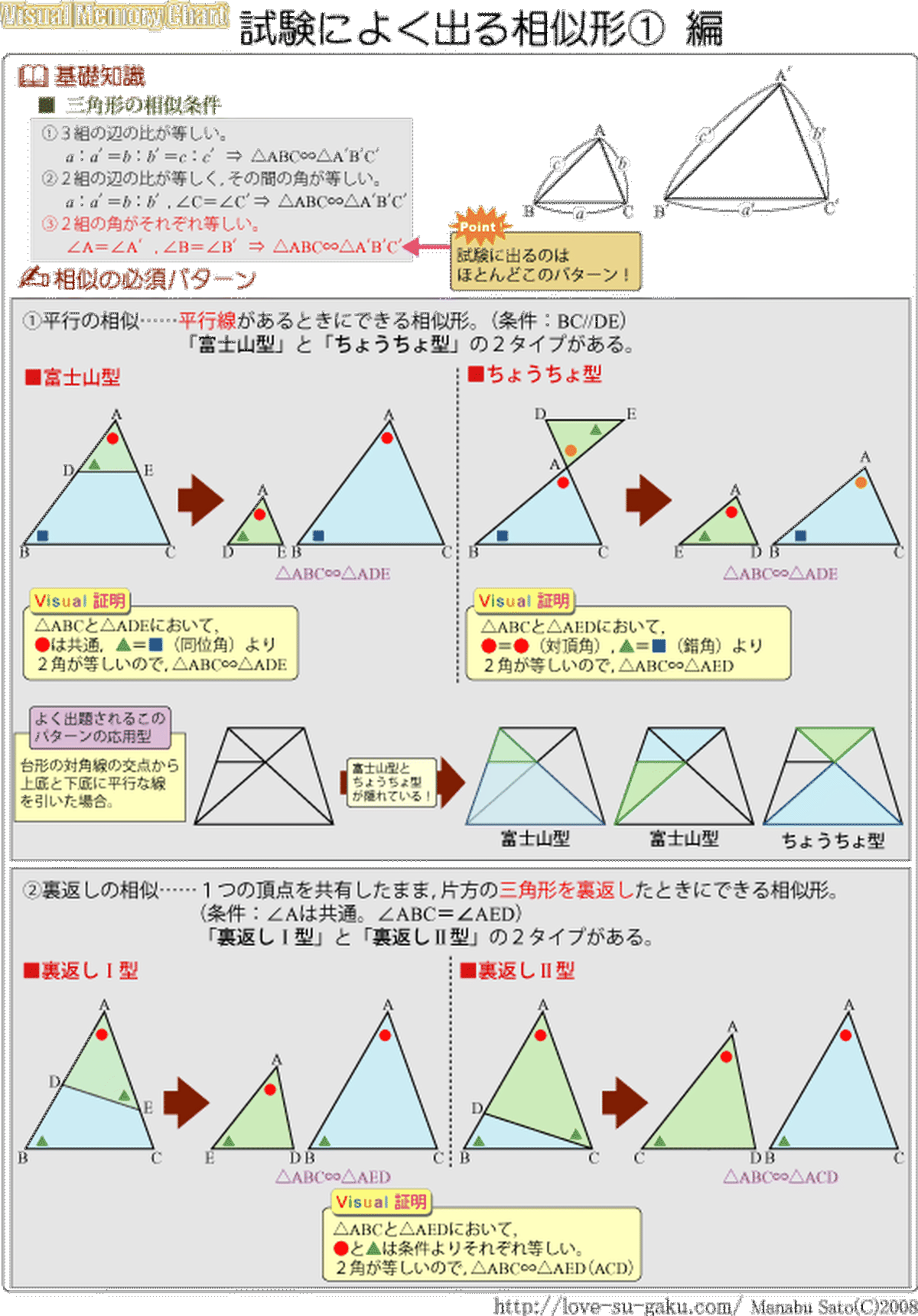
数学 試験によく出る相似形が完璧にわかるまとめ集 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru

相似の問題は2通りの解き方があります セルモ大蔵 世田谷 の塾長ブログ

相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題

相似 直角三角形

2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく

Ppt 相似条件と証明 Powerpoint Presentation Free Download Id

1

三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題

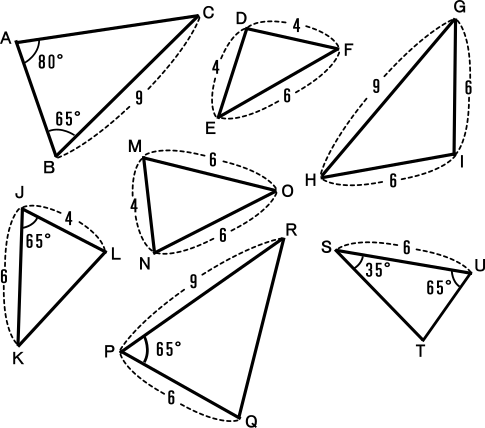
中学３年数学練習問題 三角形の相似条件の問題

三角形の相似条件

相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス

Descubre Como Resolverlo En Qanda

三角形の相似条件の解説 図形の性質

相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス

中学数学 相似の証明 その２ 中学数学の無料オンライン学習サイトchu Su

三角形の相似条件と証明問題の解き方 数学fun

相似な三角形はどれか 中学から数学だいすき

相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス

1

3角形を折る

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ

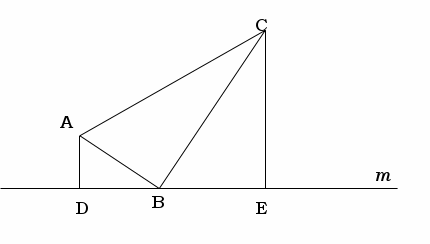
相似の証明2

Studydoctor相似な三角形の辺の比 中３数学 Studydoctor

三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

中3数学 三角形の相似条件１ ３辺の比 映像授業のtry It トライイット

三角形の相似条件と基本的な証明 無料で使える中学学習プリント

三角形の相似条件

Descubre Como Resolverlo En Qanda

三角形の相似条件

相似三角形 维基百科 自由的百科全书

Nitter

三角形の相似条件調べ Geogebra

2

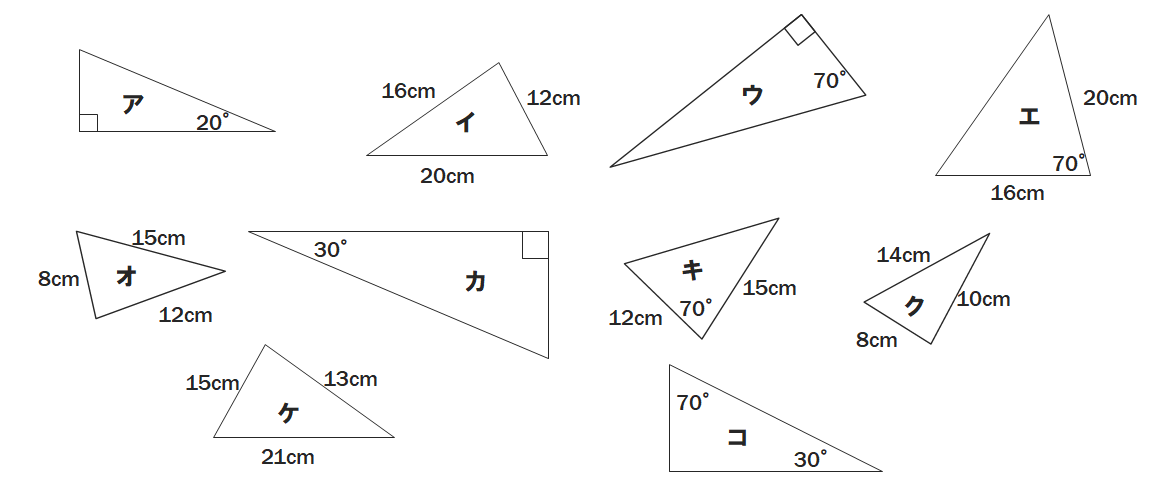
中3数学 相似な図形の線分比の定期テスト対策問題 Examee

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

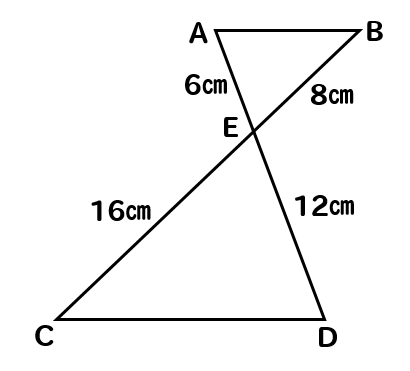
中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ

この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear

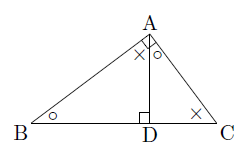
直角三角形と相似 まなびの学園

Incoming Term: 三角形 の 相似, 相似 の 三角形 条件,